事情的背景是这样子的,我们训练了一个id类为主要特征的模型,而且id的更新特别快,生命周期在3天左右,但是由于流程问题,模型只能天级更新。 模型给出一个预估分数,后续通过卡阈值来进行某些操作。上线后发现一个问题:每天的输出值分布变化较大,导致阈值不能卡固定值。
怎么去取一个动态的阈值,才能保证后续处理的数据是整体的90%左右呢?
考虑到batch normalization,通过减均值、除方差的形式来对每层的输出进行归一化,其中有moving average的技巧, 那是不是有类似的方案,可以通过滑动窗口计算分位数呢? 经过一番搜索,终于看到了一个可能可行的方案:
\[\begin{array}{l} m_0 = x_0 \\ if \quad x_i < m_{i-1} \quad m_i=m_{i-1}-\frac{\delta}{p} \\ else \quad if \quad x_i > m_{i-1} \quad m_i=m_{i-1}+\frac{\delta}{1-p} \\ else \quad m_i=m_{i-1} \end{array}\]在该方案中,$\delta$的取值比较关键,通过$\delta_i=\sigma_i\dot r$来获取,r是指定的超参,而$\sigma_i$是通过moving average计算出来的标准差。
在该链接中,作者认为r的取值从0.001到0.01都可以,但是,经过实际测试,发现r的取值较大时, 分位数的均值接近预期,但是方差会很大。尤其是分位数较小或者较大(0.99, 0.999)时,r的取值需要更小才行。
为了接近这个问题,尝试对分位数再进行moving average,结果会稳定很多。如下图所示:
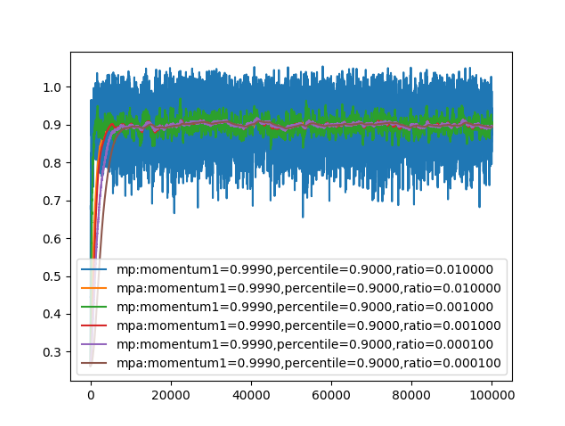
- 数据分布确定时,r决定了分位数的方差:r越小,方差越小;r越大,方差越大
- 相同的r下,分位数也会有一定影响,p(1-p)越小,准确性越差
- 建议添加一次moving average,来获取更稳定的分位数均值
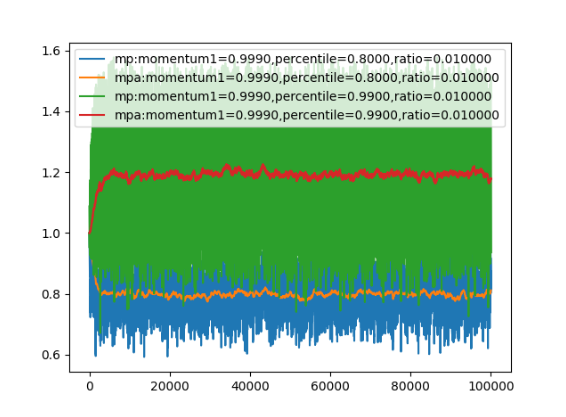
示例代码参见: