在读 Stochastic Loss Function 这篇论文的时候, 发现了一个之前从未听过的名词:Gumbel Softmax,在一探究竟的同时做下简单记录。
Gumbel-Softmax Trick
背景
在强化学习中,如果动作空间是离散的,比如上、下、左、右四个动作,通常的做法是网络输出一个四维的one-hot向量(不考虑空动作), 分别代表四个动作。比如[1,0,0,0]代表上,[0,1,0,0]代表下等等。 而具体取哪个动作呢,就根据输出的每个维度的大小,选择值最大的作为输出动作,即argmax(𝑣)。
例如网络输出的四维向量为𝑣=[−20,10,9.6,6.2],第二个维度取到最大值10,那么输出的动作就是[0,1,0,0],也就是说,这和多类别的分类任务是一个道理。 但是这种取法有个问题是不能计算梯度,也就不能更新网络。通常的做法是加softmax函数,把向量归一化,这样既能计算梯度,同时值的大小还能表示概率的含义。
将$𝑣=[−20,10,9.6,6.2]$通过softmax函数后有$𝜎(𝑣)=[0,0.591,0.396,0.013]$, 这样做不会改变动作或者说类别的选取,同时softmax倾向于让最大值的概率显著大于其他值, 比如这里10和9.6经过softmax放缩之后变成了0.591和0.396,6.2对应的概率更是变成了0.013, 这有利于把网络训成一个one-hot输出的形式,这种方式在分类问题中是常用方法。
但是这么做还有一个问题,这个表示概率的向量𝜎(𝑣)=[0,0.591,0.396,0.013]并没有真正显示出概率的含义, 因为一旦某个值最大,就选择相应的动作或者分类。比如𝜎(𝑣)=[0,0.591,0.396,0.013]和𝜎(𝑣)=[0,0.9,0.1,0]在类别选取的结果看来没有任何差别, 都是选择第二个类别,但是从概率意义上讲差别是巨大的。
对于分类问题来说,softmax已经足够使用了,但是如果我们想用这个概率值去生成样本,用于后续训练,argmax()就不再适用了。 但是直接按照概率进行采样,会导致梯度无法回传,该怎么办呢? Re-parameterization Trick就是用了解决这个问题的。
Re-parameterization Trick
从自编码器开始说起,原始的自编码器是这样子的:图像经过网络映射到embedding,decoder部分从embedding重建图像。
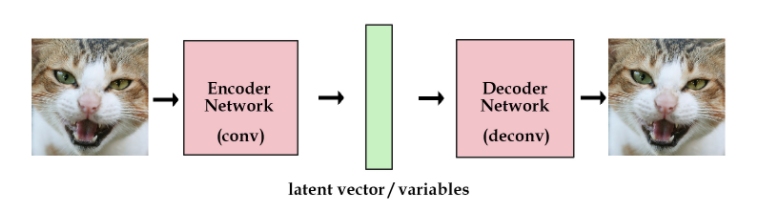
而VAE并不是直接取提取特征向量,而是提取图像的分布特征:均值和标准差,再根据均值和标准差采样生产特征向量样本,用于重建图像。
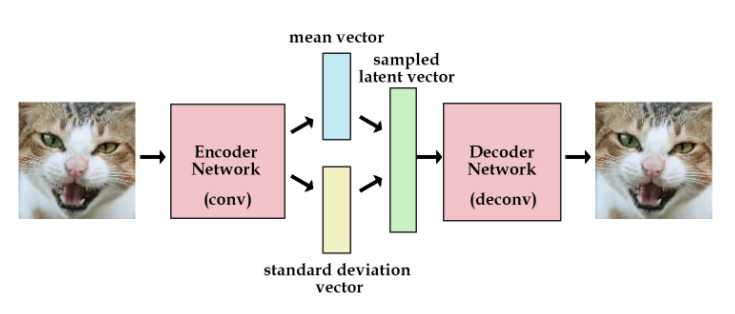
如果将采样步骤写在计算图里的话,这部分就没法计算梯度了,而重参数技巧就是用来解决这个问题的。
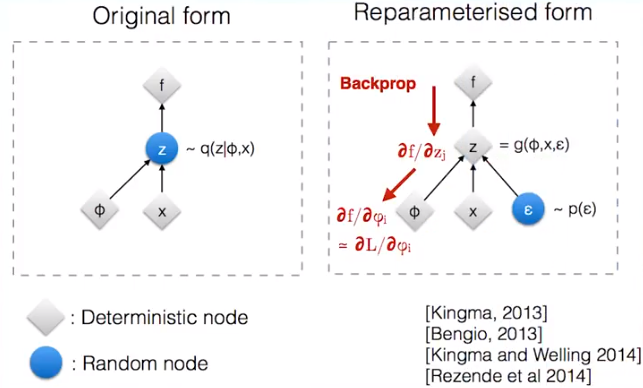
假设图中的𝑥和𝜙表示VAE中的均值和标准差向量,它们是确定性的节点。而需要输出的样本𝑧是带有随机性的节点, 重参数就是把带有随机性的𝑧变成确定性的节点,同时随机性用另一个输入节点𝜖代替。 例如,这里用正态分布采样,原本从均值为𝑥和标准差为𝜙的正态分布$𝑁(𝑥,𝜙^2)$中采样得到𝑧。 将其转化成从标准正态分布𝑁(0,1)中采样得到𝜖,再计算得到$𝑧=𝑥+𝜖⋅𝜙$。 这样一来,采样的过程移出了计算图,整张计算图就可以计算梯度进行更新了, 而新加的𝜖的输入分支不做更新,只当成一个没有权重变化的输入。
整个过程和batch normalization比较像,只不过是用随机输入代替了inference时的输入。
Gumbel-Softmax Trick
VAE的例子是一个连续分布(正态分布)的重参数,引入了一定的随机性,而离散分布的采样,就需要用到Gumbel-Softmax了。
假设每个类别的概率是$p_1, p_2, …, p_k$,可以按照如下方式依照概率对类别进行采样,称为iGumbel-Max,后续给出两者等价的证明。
\[argmax (\log p_i - \log(-\log \epsilon_i))_{i=1}^k, \epsilon_i∼U[0,1]\]也就是说,先算出各个概率的对数$\log p_i$,然后从均匀分布$U[0,1]$中采样k个随机数$\epsilon_1,…,\epsilon_k$, 把$\log(−\log \epsilon_i)$加到$\log p_i$上去,最后把最大值对应的类别抽取出来就行了。 通过这种方式,随机性转移到U[0,1]上,并且不带有未知参数,完成了离散分布的重参数过程。
为了保证可到,将GumbelMax替换为光滑版本-Gumbel Softmax
\[softmax((\log p_i − \log(−\log \epsilon_i))/\tau)^k_{i=1} ,\epsilon_i∼U[0,1]\]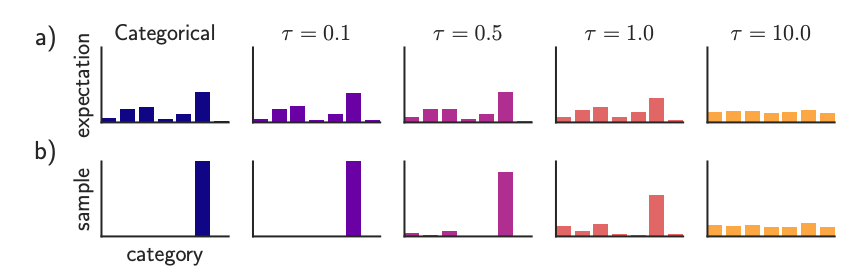
$\tau > 0$ 为退火参数,值越小,结果就越接近one-hot形式,越大就越接近等概率抽样。 有一个小技巧: 如果$p_i$是softmax的输出,那么大可不必先算出$p_i$再取对数,直接将$\log p_i$替换为$o_i$即可:
\[softmax((\log o_i − \log(−\log \epsilon_i))/\tau)^k_{i=1} ,\epsilon_i∼U[0,1]\]证明过程如下:

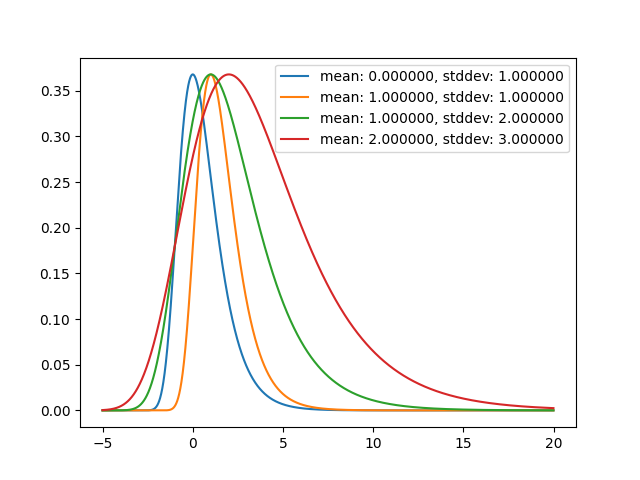
Gumbel Distribution
Gumbel Distribution 是一个关于”最大值”的概率的分布,比如已知过去100年河流的水位情况,那么gumbel分布可以用于预测明年河流的最大水位分布, 会给出每个值是”最大值”的概率。
\[z = \frac{x - \mu}{\beta}\]累积分布函数如下:
\[F(x:\mu,\beta)=e^{-e^z}\]概率密度函数如下:
\[f(x:\mu,\beta)=\frac{1}{\beta}e^{-(z + e^{-z})}\]