在海量数据中进行相似检索,是一个很常见的需求,主要用于各种召回阶段: 比如搜索场景的召回、相似视频检索等;相似物品的推荐等。 然而,现在是一个海量数据的行为,如何在短时间内完成向量距离的计算和检索,成为了一个亟待解决的问题。
我们来看一下召回面临的两个问题:
- 特征维度极大,比如bert特征是768维;user-item的click矩阵可以达到百万、千万维
- item数量巨大,进行检索十分困难
针对这两个问题,有着不同的优化方案, 第一个问题就是特征降维; 第二个问题是优化检索方案-减少需要检索的数量。
特征降维
PCA(Principal Component Analysis)
PCA(Principal Component Analysis) 是一种常见的数据分析方式,常用于高维数据的降维,可用于提取数据的主要特征分量。
Minhashing
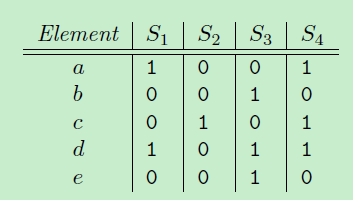
以上图为例, 物品集合为{a,b,c,d,e}, 用户行为为 S1 = {a, b}, S2 = {c}, S3 = {b, d, e}, S4 = {a, c, d}。 如果在文本数据中,Si可以视为每个文本的bow向量,{a,b,c,d,e}可以视为词典集合。
Minhashing是怎么做的呢?
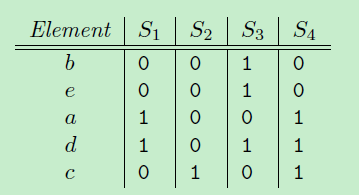
把原来元素{a, b, c, d, e} 顺序随机重排,比如下图, 排序结果为{b, e, a, d, c}, 定义一个函数h:计算集合S最小的minhash值,就是在这种顺序下最先出现1的元素。 那么h(S1) = a, h(S2)=c, h(S3)=b, h(S4)=a;
如果进行n重排的话,就会有n个minhash函数,{h1(S), h2(S)…, hn(S)}, 那原来每个高维集合,就会被降到n维空间,比如S1->{h1(S1), h2(S1)…, hn(S1)}。
但是在实际操作中,n的数量也是非常巨大的,整体重排需要的时间也很多, 通常会用若干随机哈希函数代替重排过程。 比如$h(x) = (i + 1) % 5 $,i表示对应的索引,从1开始,那么会有如下结果:
\[h_{S_1}(a) = 2 \\ h_{S_1}(d) = 0 \\ h_{S_2}(c) = 4 \\ h_{S_3}(b) = 3 \\ h_{S_3}(d) = 0 \\ h_{S_3}(e) = 1 \\ h_{S_4}(a) = 1 \\ h_{S_4}(c) = 4 \\ h_{S_4}(d) = 0 \\ minhash(h_{S_1}) = d \\ minhash(h_{S_2}) = c \\ minhash(h_{S_3}) = d \\ minhash(h_{S_4}) = d\]检索优化
- 基于树的方法
- KD树是其下的经典算法。一般而言,在空间维度比较低时,KD树的查找性能还是比较高效的;但当空间维度较高时,该方法会退化为暴力枚举,性能较差,这时一般会采用下面的哈希方法或者矢量量化方法。
- 哈希方法
- LSH(Locality-Sensitive Hashing)是其下的代表算法。文献[7]是一篇非常好的LSH入门资料。
- 对于小数据集和中规模的数据集(几个million-几十个million),基于LSH的方法的效果和性能都还不错。这方面有2个开源工具FALCONN和NMSLIB。
- 矢量量化方法
- 矢量量化方法,即vector quantization。在矢量量化编码中,关键是码本的建立和码字搜索算法。比如常见的聚类算法,就是一种矢量量化方法。而在相似搜索中,向量量化方法又以PQ方法最为典型。
- 对于大规模数据集(几百个million以上),基于矢量量化的方法是一个明智的选择,可以用用Faiss开源工具。
KDTree
kd 树是一种对k维特征空间中的实例点进行存储以便对其快速检索的树形数据结构。 kd树是二叉树,核心思想是对 k 维特征空间不断切分: 假设特征维度是768,对于(0,1,2,…,767)中的每一个维度,以中值递归切分。 这样构造的树,每一个节点是一个超矩形, 小于结点的样本划分到左子树,大于结点的样本划分到右子树。 树构造完毕后,最终检索过程如下: -(1)从根结点出发,递归地向下访问kd树。 若目标点当前维的坐标小于切分点的坐标,移动到左子树,否则移动到右子树,直至到达叶结点; -(2)以此叶结点为“最近点”,递归地向上回退, 查找该结点的兄弟结点中是否存在更近的点,若存在则更新“最近点”,否则回退; 未到达根结点时继续执行(2) -(3)回退到根结点时,搜索结束。
对KD树选择从哪一维度进行开始划分的标准,采用的是求每一个维度的方差,然后选择方差最大的那个维度开始划分。 这里有一个比较有意思的问题是:为何要选择方差作为维度划分选取的标准? 我们都知道,方差的大小可以反映数据的波动性。 方差大表示数据波动性越大,选择方差最大的开始划分空间,可以使得所需的划分面数目最小, 反映到树数据结构上,可以使得我们构建的KD树的树深度尽可能的小。
kd树在维数小于20时效率最高,一般适用于训练实例数远大于空间维数时的k近邻搜索; 当空间维数接近训练实例数时,它的效率会迅速下降,几乎接近线形扫描。
BallTree
为了解决kd树在样本特征维度很高时效率低下的问题, 研究人员提出了“球树“BallTree。 KD 树沿坐标轴分割数据,BallTree将在一系列嵌套的超球面上分割数据, 即使用超球面而不是超矩形划分区域。 具体而言,BallTree 将数据递归地划分到由质心 C 和 半径 r 定义的节点上, 以使得节点内的每个点都位于由质心C和半径 r 定义的超球面内。 通过使用三角不等式|X+Y|<=|x| + |Y|减少近邻搜索的候选点数。
Annoy(Approximate Nearest Neighbors Oh Yeah)
Annoy 同样通过建立一个二叉树来使得每个点查找时间复杂度是O(log n), 和kd树不同的是,annoy没有对k维特征进行切分。 每次都是*随机选择两个点,以这两个节点为初始中心节点,执行聚类数为2的kmeans过程,最终产生收敛后两个聚类中心点。** 这两个聚类中心点之间连一条线段(灰色短线), 建立一条垂直于这条灰线,并且通过灰线中心 点的线(黑色粗线)。这条黑色粗线把数据空间分成两部分。 在多维空间的话,这条黑色粗线可以看成等距垂直超平面。

在划分的子空间内进行不停的递归迭代继续划分,直到每个子空间最多只剩下K个数据节点。
最终原始数据会形成类似下面这样一个二叉树结构。 二叉树底层是叶子节点记录原始数据节点,其他中间节点记录的是分割超平面的信息。 Annoy建立这样的二叉树结构是希望满足这样的一个假设: 相似的数据节点应该在二叉树上位置更接近, 一个分割超平面不应该把相似的数据节点分割二叉树的不同分支上。
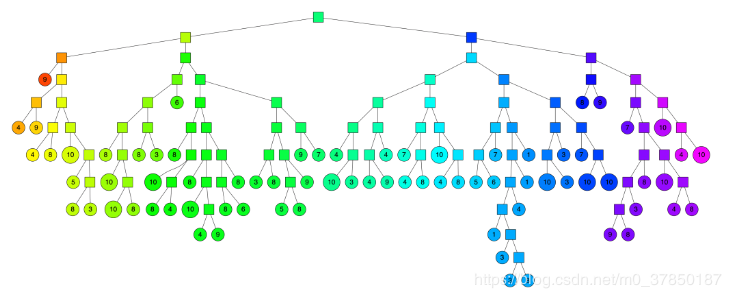
查询过程
如何进行对一个数据点进行查找相似节点集合呢? 查找的过程就是不断看他在分割超平面的哪一边。 从二叉树索引结构来看,就是从根节点不停的往叶子节点遍历的过程。 通过对二叉树每个中间节点(分割超平面相关信息)和查询数据节点进行相关计算 来确定二叉树遍历过程是往这个中间节点左孩子节点走还是右孩子节点走。 通过以上方式完成查询过程。
然而实际情况并不会这么简单,
- 如果查询过程最终落到叶子节点的数据节点数小于 我们需要的Top N相似邻居节点数目怎么办?
- 两个相近的数据节点划分到二叉树不同分支上怎么办? 方案如下: (1) 如果分割超平面的两边都很相似,那可以两边都遍历 (2) 建立多棵二叉树树,构成一个森林,每个树建立机制都如上面所述那样 (3) 采用优先队列机制:采用一个优先队列来遍历二叉树,从根节点往下的路径,根据查询节点与当前分割超平面距离(margin)进行排序。
每棵树都返回一堆近邻点后,如何得到最终的Top N相似集合呢? 首先所有树返回近邻点都插入到优先队列中,求并集去重, 然后计算和查询点距离, 最终根据距离值从近距离到远距离排序, 返回Top N近邻节点集合。
LSH(Locality-Sensitive Hashing)
LSH为我们提供了一种在海量的高维数据集中查找与查询数据点(query data point) 近似最相邻的某个或某些数据点。需要注意的是, LSH并不能保证一定能够查找到与query data point最相邻的数据, 而是减少需要匹配的数据点个数的同时保证查找到最近邻的数据点的概率很大。
基本思想是这样的: 将原始数据空间中的两个相邻数据点通过相同的映射或投影变换(projection)后, 这两个数据点在新的数据空间中仍然相邻的概率很大, 而不相邻的数据点被映射到同一个桶的概率很小。 也就是说,如果我们对原始数据进行一些hash映射后, 我们希望原先相邻的两个数据能够被hash到相同的桶内, 具有相同的桶号。 对原始数据集合中所有的数据都进行hash映射后, 我们就得到了一个hash table, 这些原始数据集被分散到了hash table的桶内, 每个桶会落入一些原始数据,属于同一个桶内的数据就有很大可能是相邻的, 当然也存在不相邻的数据被hash到了同一个桶内。 因此,如果我们能够找到这样一些hash functions, 使得经过它们的哈希映射变换后, 原始空间中相邻的数据落入相同的桶内的话, 那么我们在该数据集合中进行近邻查找就变得容易了, 我们只需要将查询数据进行哈希映射得到其桶号, 然后取出该桶号对应桶内的所有数据, 再进行线性匹配即可查找到与查询数据相邻的数据。 换句话说,我们通过hash function映射变换操作, 将原始数据集合分成了多个子集合, 而每个子集合中的数据间是相邻的且该子集合中的元素个数较小, 因此将一个在超大集合内查找相邻元素的问题转化为了在一个很小的集合内查找相邻元素的问题, 显然计算量下降了很多。
那具有怎样特点的hash functions才能够使得原本相邻的两个数据点经过hash变换后会落入相同的桶内? 这些hash function需要满足以下两个条件:
- 如果d(x,y) ≤ d1, 则h(x) = h(y)的概率至少为p1;
- 如果d(x,y) ≥ d2, 则h(x) = h(y)的概率至多为p2;
其中d(x,y)表示x和y之间的距离,d1 < d2, h(x)和h(y)分别表示对x和y进行hash变换。 满足以上两个条件的hash functions称为(d1,d2,p1,p2)-sensitive。 而通过一个或多个(d1,d2,p1,p2)-sensitive的hash function对原始数据集合进行hashing 生成一个或多个hash table的过程称为Locality-sensitive Hashing。
查找过程
使用LSH进行对海量数据建立索引(Hash table)并通过索引来进行近似最近邻查找的过程如下:
- 离线建立索引
- 选取满足(d1,d2,p1,p2)-sensitive的LSH hash functions;
- 根据对查找结果的准确率(即相邻的数据被查找到的概率)确定hash table的个数L, 每个table内的hash functions的个数K,以及跟LSH hash function自身有关的参数;
- 将所有数据经过LSH hash function哈希到相应的桶内,构成了一个或多个hash table;
- 在线查找
- 将查询数据经过LSH hash function哈希得到相应的桶号;
- 将桶号中对应的数据取出;(为了保证查找速度,通常只需要取出前2L个数据即可);
- 计算查询数据与这2L个数据之间的相似度或距离,返回最近邻的数据;
增强LSH(Amplifying LSH)
通过LSH hash functions我们能够得到一个或多个hash table, 每个桶内的数据之间是近邻的可能性很大。 我们希望原本相邻的数据经过LSH hash后, 都能够落入到相同的桶内, 而不相邻的数据经过LSH hash后, 都能够落入到不同的桶中。 如果相邻的数据被投影到了不同的桶内,我们称为false negtive; 如果不相邻的数据被投影到了相同的桶内,我们称为false positive。 因此,我们在使用LSH中,我们希望能够尽量降低false negtive rate和false positive rate。
为了达到这个目标,通常有两种方案:
- 在一个hash table内使用更多的LSH hash function
- 建立多个hash table
以及一些常用方法:
- 多个独立的hash table: 每次选用k个LSH hash function(同属于一个LSH function family)就得到了一个hash table,重复多次,即可创建多个hash table。多个hash table的好处在于能够降低false positive rate。
- AND 操作: 从同一个LSH function family中挑选出k个LSH function,H(X) = H(Y)有且仅当这k个Hi(X) = Hi(Y)都满足。也就是说只有当两个数据的这k个hash值都对应相同时,才会被投影到相同的桶内,只要有一个不满足就不会被投影到同一个桶内。 AND与操作能够使得找到近邻数据的p1概率保持高概率的同时降低p2概率,即降低了falsenegtiverate。
- OR 操作: 从同一个LSH function family中挑选出k个LSH function,H(X) = H(Y)有且仅当存在一个以上的Hi(X) = Hi(Y)。也就是说只要两个数据的这k个hash值中有一对以上相同时,就会被投影到相同的桶内,只有当这k个hash值都不相同时才不被投影到同一个桶内。 OR或操作能够使得找到近邻数据的p1概率变的更大(越接近1)的同时保持p2概率较小,即降低了false positive rate。
- AND和OR的级联 将与操作和或操作级联在一起,产生更多的hahs table,这样的好处在于能够使得p1更接近1,而p2更接近0。
除了上面介绍的增强LSH的方法外,有时候我们希望将多个LSH hash function得到的hash值组合起来,在此基础上得到新的hash值,这样做的好处在于减少了存储hash table的空间。下面介绍一些常用方法:
-
求模运算 new hash value = old hash value % N
-
随机投影 假设通过k个LSH hash function得到了k个hash值:h1, h2…, hk。那么新的hash值采用如下公式求得:
new hash value = h1r1 + h2r2 + … + hk*rk,其中r1, r2, …, rk是一些随机数。
- XOR异或
假设通过k个LSH hash function得到了k个hash值:h1, h2…, hk。那么新的hash值采用如下公式求得:
new hash value = h1 XOR h2 XOR h3 … XOR hk
LSH Family
d(x,y)表示x,y之间的一个距离度量,并不是所有的距离度量都有能够满足locality-sensitive的哈希函数。 通常有以下几种距离度量方式及哈希函数:
- Jaccard distance,对应的LSH hash function为:minhash,其是(d1,d2,1-d1,1-d2)-sensitive的。
- Hamming Distance:两个具有相同长度的向量中对应位置处值不同的次数, hash function为:H(V) = 向量V的第i位上的值,其是(d1,d2,1-d1/d,1-d2/d)-sensitive
-
cosine distance,hash function为:H(V) = sign(V·R), R是一个随机向量。V·R可以看做是将V向R上进行投影操作。 利用随机的超平面(random hyperplane)将原始数据空间进行划分, 每一个数据被投影后会落入超平面的某一侧,经过多个随机的超平面划分后, 原始空间被划分为了很多cell,而位于每个cell内的数据被认为具有很大可能是相邻的 (即原始数据之间的cosine distance很小)。 其是(d1,d2,(180-d1)180,(180-d2)/180)-sensitive的。
-
Euclidean distance 是衡量D维空间中两个点之间的距离的一种距离度量方式。 对应的LSH hash function为:H(V) = |V·R + b| / a, R是一个随机向量,a是桶宽,b是一个在[0,a]之间均匀分布的随机变量。 V·R可以看做是将V向R上进行投影操作。其是(a/2,2a,1/2,1/3)-sensitive的。
理解:将原始数据空间中的数据投影到一条随机的直线(random line)上, 并且该直线由很多长度等于a的线段组成, 每一个数据被投影后会落入该直线上的某一个线段上(对应的桶内), 将所有数据都投影到直线上后, 位于同一个线段内的数据将被认为具有很大可能是相邻的( 即原始数据之间的Euclidean distance很小)。
Simhash
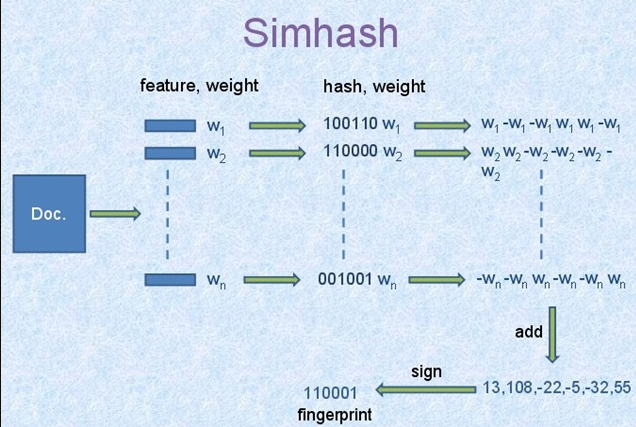
simhash在工业界引起很大注意力是因为google 07那篇文章, 把Simhash技术引入到海量文本去重领域。 google 通过Simhash把一篇文本映射成64bits的二进制串。下面是具体示意图: 文档每个词有个权重,同时哈希成一个二进制串。文档最终的签名是各个词签名的加权和。 如果两篇文档相同,则他们simhash签名汉明距离小于等于3。
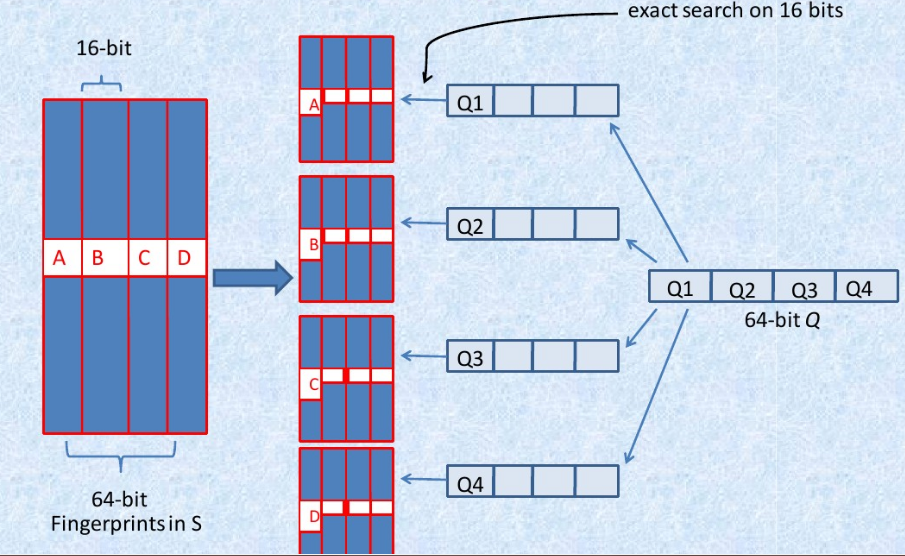
通过simhash过程,将很长的文本表示为64位的二进制串,其实是在解决第二个问题,对特征进行降维。 然而,第一个问题还是没有解决。 不过,考虑到应用场景及限制–如果两篇文档相同,则他们simhash签名汉明距离小于等于3, 作者将64位分为4份(slot),对每份进行hash,这样的话,只有至少一个slot相同,两个文档才有可能重复。 在一定程度上降低了计算量。
HNSW(Hierarchcal Navigable Small World graphs)(github)
和前几种算法不同,HNSW(Hierarchcal Navigable Small World graphs)是基于图存储的数据结构。 参考该博客
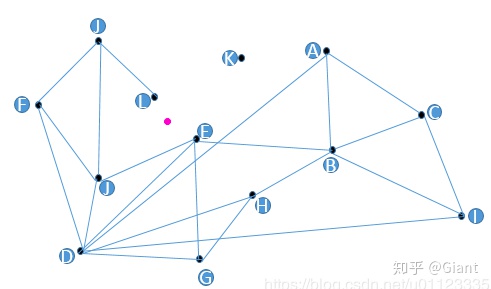
假设我们现在有13个2维数据向量, 我们把这些向量放在了一个平面直角坐标系内, 隐去坐标系刻度,它们的位置关系如上图所示。
朴素查找法:
不少人脑子里都冒出过这样的朴素想法,把某些点和点之间连上线,构成一个查找图,存储备用; 当查找与粉色点最近的一点时我从任意一个黑色点出发,计算它和粉色点的距离,与这个任意黑色点有连接关系的点我们称之为“友点”(直译), 然后计算这个黑色点的所有“友点”与粉色点的距离,从所有“友点”中选出与粉色点最近的一个点, 把这个点作为下一个进入点,继续按照上面的步骤查找下去。 如果当前黑色点对粉色点的距离比所有“友点”都近,终止查找。
朴素想法之所以叫朴素想法就是因为它的缺点非常多。
- 首先,我们发现图中的K点是无法被查询到的,因为K点没有友点,怎么办?
- 其次,如果我们要查找距离粉色点最近的两个点,而这两个近点之间如果没有连线, 那么将大大影响效率(比如L和E点,如果L和E有连线,那么我们可以轻易用上述方法查出距离粉色点最近的两个点),怎么办?
- 最后一个大问题,D点真的需要这么多“友点”吗?谁是谁的友点应该怎么确定呢?
为了解决上述问题,我们有如下规定:
- 1)图中每个点都有“友点”: 防止某些点无法到达
- 2)在构图时所有距离相近(相似)到一定程度的向量必须互为友点: 近点没有连线的话,查询效率会很低
- 3)图中所有连线的数量最少:友点太多,会影响查找效率
NSW算法
在图论中有一个很好的剖分法则专门解决上一节中提到的朴素想法的缺陷问题——德劳内(Delaunay)三角剖分算法, 这个算法可以达成如下要求:1,图中每个点都有“友点”。2,相近的点都互为“友点”。3,图中所有连接(线段)的数量最少。 效果如下图。

但NSW没有采用德劳内三角剖分法来构成德劳内三角网图, 原因之一是德劳内三角剖分构图算法时间复杂度太高,换句话说,构图太耗时。 原因之二是德劳内三角形的查找效率并不一定最高, 如果初始点和查找点距离很远的话我们需要进行多次跳转才能查到其临近点, 需要“高速公路”机制(Expressway mechanism, 这里指部分远点之间拥有线段连接,以便于快速查找)。 在理想状态下,我们的算法不仅要满足上面三条需求,还要算法复杂度低,同时配有高速公路机制的构图法。
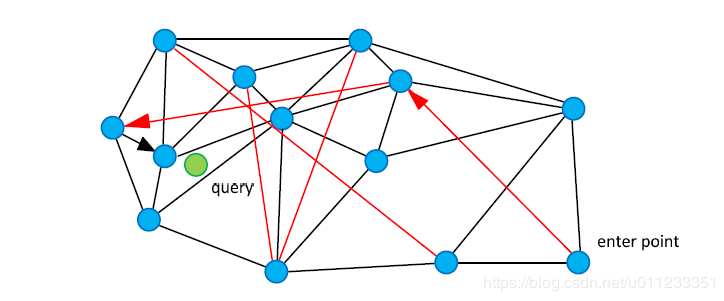
NSW论文中配了这样一张图,黑色是近邻点的连线,红色线就是“高速公路机制”了。 我们从enter point点进入查找,查找绿色点临近节点的时候,就可以用过红色连线“高速公路机制”快速查找到结果。
那么,NSW是如何构建图结构的呢?
向图中逐个插入点,插入一个全新点时,通过朴素想法中的朴素查找法(通过计算“友点”和待插入点的距离来判断下一个进入点是哪个点) 查找到与这个全新点最近的m个点(m由用户设置),连接全新点到m个点的连线。
构图算法是逐点随机插入的,这就意味着在图构建的早期,很有可能构建出“高速公路”。 假设我们现在要构成10000个点组成的图,设置m=4(每个点至少有4个“友点”), 这10000个点中有两个点,p和q,他们俩坐标完全一样。 假设在插入过程中我们分别在第10次插入p,在第9999次插入q,请问p和q谁更容易具有“高速公路”? 答:因为在第10次插入时,只见过前9个点,故只能在前9个点中选出距离最近的4个点(m=4)作为“友点”, 而q的选择就多了,前9998个点都能选,所以q的“友点”更接近q,p的早期“友点”不一定接近p,所以p更容易具有“高速公路”。 结论:一个点,越早插入就越容易形成与之相关的“高速公路”连接,越晚插入就越难形成与之相关的“高速公路”连接。 所以这个算法设计的妙处就在于扔掉德劳内三角构图法,改用“无脑添加”(NSW朴素插入算法), 降低了构图算法时间复杂度的同时还带来了数量有限的“高速公路”,加速了查找。
NSW算法的朴素构思就讲到这里了,下面我们来说说优化。
一.在查找的过程中,为了提高效率,我们可以建立一个废弃列表, 在一次查找任务中遍历过的点不再遍历。 在一次查找中,已经计算过这个点的所有友点距离查找点的距离,并且已经知道正确的跳转方向了, 这些结果是唯一的,没有必要再去做走这个路径,因为这个路径会带给我们同样的重复结果,没有意义。
二.在查找过程中,为了提高准确度,我们可以建立一个动态列表, 把距离查找点最近的n个点存储在表中,并行地对这n个点进行同时计算“友点”和待查找点的距离, 在这些“友点”中选择n个点与动态列中的n个点进行并集操作,在并集中选出n个最近的友点,更新动态列表。
设待查找q点的m个近邻点。使用伪代码描述如下:
- 随机选一个点作为初始进入点,建立空废弃表g和动态列表c,g是变长的列表,c是定长为s的列表(s>m),将初始点放入动态列表c(附上初始点和待查找q的距离信息),制作动态列表的影子列表c’。
- 对动态列表c中的所有点并行找出其“友点”,查看这些“友点”是否存储在废弃表g中,如果存在,则丢弃,如不存在,将这些剩余“友点”记录在废弃列表g中(以免后续重复查找,走冤枉路)。
- 并行计算这些剩余“友点”距离待查找点q的距离,将这些点及其各自的距离信息放入c。
- 对动态列表c去重,然后按距离排序(升序),储存前s个点及其距离信息。
- 查看动态列表c和c’是否一样,如果一样,结束本次查找,返回动态列表中前m个结果。如果不一样,将c’的内容更新为c的内容,执行第2步。
跳表
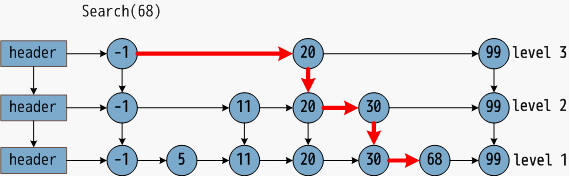
HNSW
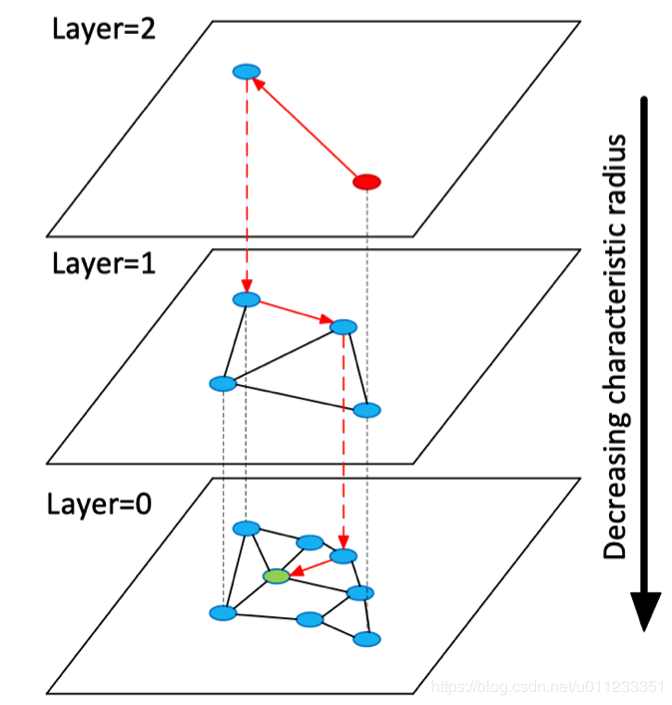
论文中的一张示意图即可看懂作者malkov的意思。 第0层中,是数据集中的所有点,你需要设置一个常数ml,通过公式$floor(-ln(uniform(0,1)) \times ml)$来计算这个点可以深入到第几层。
- 第0层中包含图中所有节点
- 向上节点数依次减少,遵循指数衰减概率分布
- 建图时新加入的节点由指数衰减概率函数得出该点最高投影到第几层
- 从最高的投影层向下的层中该点均存在
- 搜索时从上向下依次查询
插入构图的时候:
- 先计算这个点可以深入到第几层,
- 自顶层向q的层数l逼近搜索,一直到l+1,每层寻找当前层q最近邻的1个点
- 自l层向底层逼近搜索,每层寻找当前层q最近邻的efConstruction个点赋值到集合W
- 在W中选择q最近邻的M个点作为neighbors双向连接起来
- 检查每个neighbors的连接数,如果大于Mmax,则需要缩减连接到最近邻的Mmax个
需要注意的是第5点,每个节点的出度是有上限的,这样可以保证搜索的效率, 这里就需要针对某些边进行裁剪,那么该裁剪哪些边呢? Fast Approximate Nearest Neighbour Graphs一文中给出了裁边的原则:
edge(p1, p2) occludes edge(p1, p3) if d(p1, p2) < d(p1, p3) and d(p2, p3) < d(p1, p3)
PQ(Product Quantization)
在介绍PQ算法前,先简要介绍vector quantization。 在信息论里,quantization是一个被充分研究的概念。 Vector quantization定义了一个量化器quantizer,即一个映射函数q, 它将一个D维向量x转换码本cookbook中的一个向量,这个码本的大小用k表示。 一般来说,码本的大小k一般会是2的幂次方,那么就可以用$log_2k$bit对应的向量来表示码本的每个值。
PQ乘积量化能够加速索引的原理:即将全样本的距离计算,转化为到子空间类中心的距离计算。
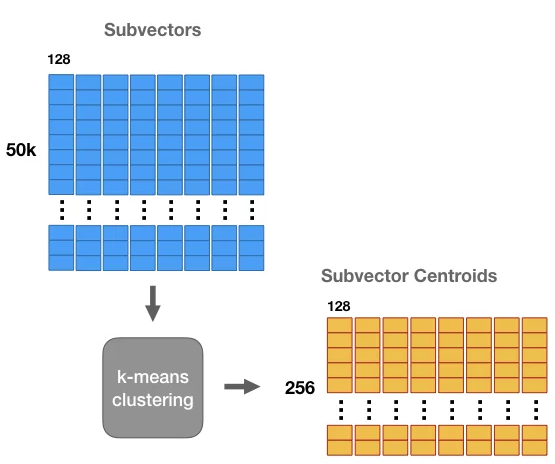
假设原始向量是1024维,可以把它拆解成8个子向量,每个子向量128维。 然后对每个字向量的全部50k数据分别作Kmeans计算,假设设置Kmeans的K为256。
注意到每组子向量有其256个中心点,我们可以中心点的 ID 来表示每组子向量中的每个向量。 中心点的ID只需要8位来保存即可。 这样,初始一个由32位浮点数组成的1,024维向量,可以转化为8个8位整数组成。如下图
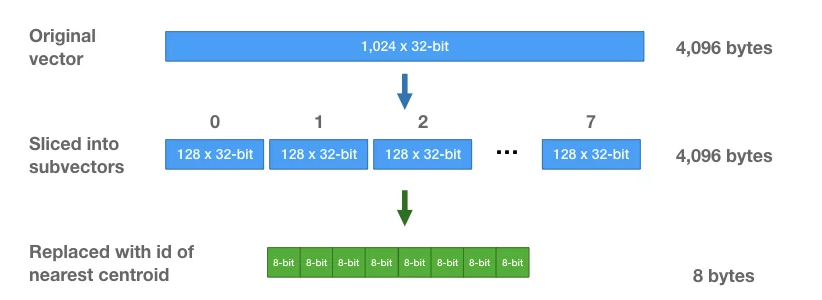
进行向量压缩之后,距离的计算也有两种方式,一种是SDC(symmetric distance computation),另一种是ADC(asymmetric distance computation), 区别主要在于是否要对查询向量x做量化: x是查询向量(query vector),y是数据集中的某个向量,目标是要在数据集中找到x的相似向量。
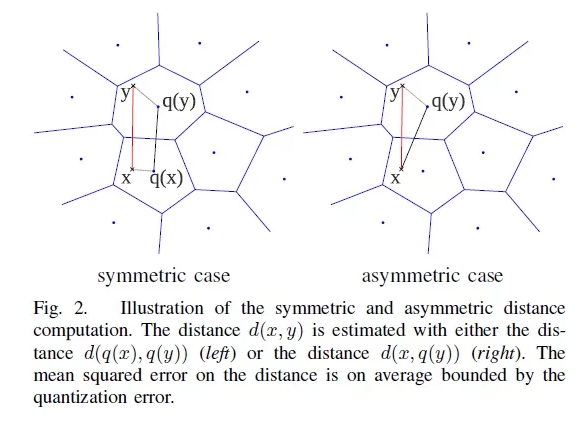
SDC算法:先用PQ量化器对x和y表示为对应的中心点q(x)和q(y),然后用公式1来近似d(x,y).
\[\hat{d}(x,y)= d(q(x),q(y)) = \sqrt{\sum_jd(q_j(x), q_j(y))^2} \tag{1}\]补充:
- 为提高计算速度,一般会提前算好$d(c_{ji},c_{ji}′)^2$,然后在检索时就是查表,以O(1)的复杂度查出结果。
- $\hat{d}(x,y)$也是$d(x,y)$的近似计算,一般会先用相似计算方法选出top N近邻,然后再做rerank以拿到最终的近邻排序结果。
ADC算法:只对y表示为对应的中心点q(y),然后用下述公式2来近似d(x,y)。
\[\hat{d}(x,y)= d(x,q(y)) = \sqrt{\sum_jd(u_j(x), q_j(y))^2} \tag{2}\]倒排乘积量化(IVFPQ)
倒排PQ乘积量化(IVFPQ)是PQ乘积量化的更进一步加速版。 brute-force搜索的方式是在全空间进行搜索,为了加快查找的速度, 几乎所有的ANN方法都是通过对全空间分割,将其分割成很多小的子空间,在搜索的时候,通过某种方式,快速锁定在某一(几)子空间,然后在该(几个)子空间里做遍历。 在上一小节可以看出,PQ乘积量化计算距离的时候,距离虽然已经预先算好了,但是对于每个样本到查询样本的距离,还是得老老实实挨个去求和相加计算距离。 但是,实际上我们感兴趣的是那些跟查询样本相近的样本,也就是说老老实实挨个相加其实做了很多的无用功, 如果能够通过某种手段快速将全局遍历锁定为感兴趣区域,则可以舍去不必要的全局计算以及排序。 倒排PQ乘积量化的”倒排“,正是这样一种思想的体现,在具体实施手段上,采用的是通过聚类的方式实现感兴趣区域的快速定位, 在倒排PQ乘积量化中,聚类可以说应用得淋漓尽致。
在PQ乘积量化之前,增加了一个粗量化过程。 具体地,先对N个训练样本采用K-Means进行聚类,这里聚类的数目一般设置得不应过大,一般设置为1024差不多, 这种可以以比较快的速度完成聚类过程。 得到了聚类中心后,针对每一个样本$x_i$,找到其距离最近的类中心$c_i$后,两者相减得到样本$x_i$的残差向量($x_i-c_i$), 后面剩下的过程,就是针对($x_i-c_i$)的PQ乘积量化过程,此过程不再赘述。
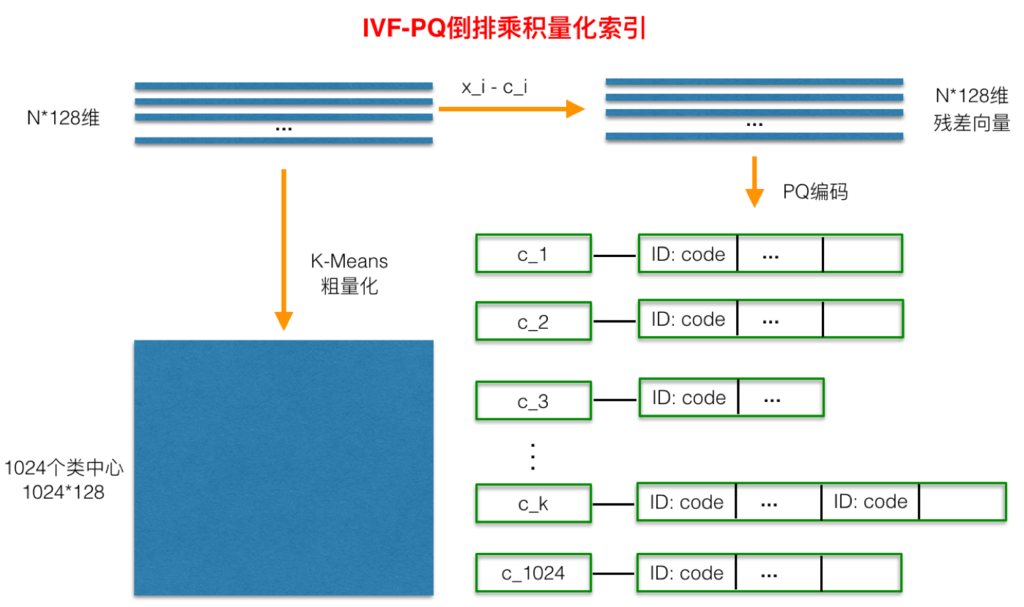
在查询的时候,通过相同的粗量化,可以快速定位到查询向量属于哪个$c_i$(即在哪一个感兴趣区域), 然后在该感兴趣区域按上面所述的PQ乘积量化距离计算方式计算距离。
参考文献
- http://yongyuan.name/blog/ann-search.html
- https://zhuanlan.zhihu.com/p/138311261
- http://vividfree.github.io/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/2017/08/05/understanding-product-quantization
- http://www.fabwrite.com/productquantization
- https://blog.csdn.net/m0_37850187/article/details/92712490
- https://blog.csdn.net/hero_fantao/article/details/70245284
- https://zhuanlan.zhihu.com/p/80552211?utm_source=wechat_session
- https://blog.csdn.net/u011233351/article/details/85116719
- https://zhuanlan.zhihu.com/p/152522906
- https://zhuanlan.zhihu.com/p/46164294
- https://www.jianshu.com/p/e6af33fd8e27
- https://blog.csdn.net/icvpr/article/details/12342159
- https://blog.csdn.net/chichoxian/article/details/80290782
- https://www.cnblogs.com/wt869054461/p/8148940.html