上次介绍过了Style Transfer的一系列文章,但是可以发现,哪怕是最后一篇ADIN,也已经是2017年了。 那么,近几年大家都在做什么呢?
搜索关键词的时候,发现大家都在做Photorealistic Style Transfer,对目标图片的真实感有了更高的要求。
正如Style Transfer的基础是Image Style Transfer Using Convolutional Neural Networks 一样, Photorealistic Style Transfer也有其理论基础,即 Bilateral Filter (双边滤波器)。
Bilateral Filter
在cv领域,对图像进行滤波是常见的操作,通用公式如下: \(I^o_p = \frac{\sum_qI(p)w(p, q)}{\sum_qw(p, q)} \tag{1}\)
这里$I(p)$代表图像,p,q是图像上的坐标,$w(p,q)$代表与位置相关的权重。 大多数滤波器的区别就在于权重的选择。
以高斯滤波来说, \(w(p,q) = G_{\sigma}(|| p - q ||) = \frac{1}{2\pi \sigma^2}exp(-\frac{|| p - q || ^ 2}{2\sigma^2}) \tag{2}\)
只考虑了p,q的距离,距离越远,权重越低;这样可以用来做平滑,但是会导致边缘被摸糊掉。
# for pixel[x][y]
new_pixel[x][y] = 0
k = 0
for i in range(-r, r + 1):
for j in range(-r, r + 1):
new_pixel[x][y] += pixel[i + x][j + y] * c[i][j]
k += c[i][j]
new_pixel[x][y] /= k
而双边滤波则同时考虑了p,q两点的距离和像素值相似程度: 距离越近、相似程度越高,权重越大。 \(w(p,q) = G_{\sigma_s}(||p-q|)G_{\sigma_r}(|I(p) - I(q)|) \tag{3}\)
# for pixel[x][y]
new_pixel[x][y] = 0
k = 0
for i in range(-r, r + 1):
for j in range(-r, r + 1):
w = c[i][j] * s(pixel[x][y], pixel[i + x][j + y])
new_pixel[x][y] += pixel[i + x][j + y] * w
k += w
new_pixel[x][y] /= k
这样的话,同时考虑空域信息和灰度相似性,
达到保边去噪的目的。具有简单、非迭代、局部的特点。
但是由于保存了过多的高频信息,对于彩色图像里的高频噪声,
双边滤波器不能够干净的滤掉,只能够对于低频信息进行较好的滤波。
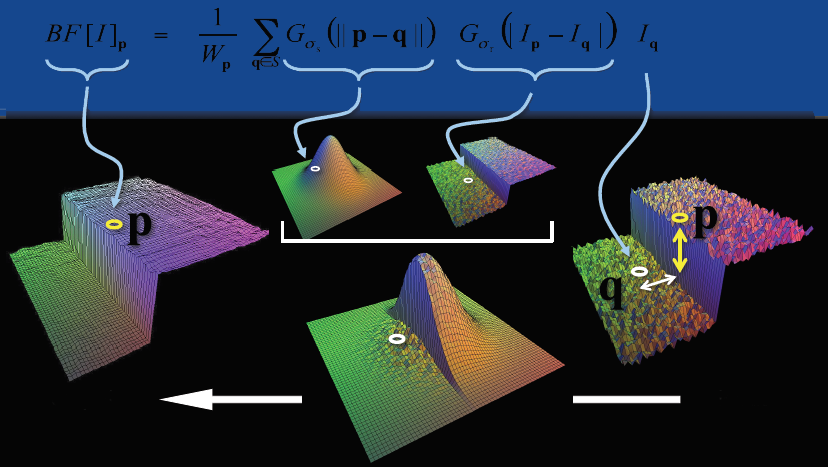
然而,在保留边缘信息的时候,双边滤波的计算量也增加了许多。
有没有办法进行加速呢?
考虑到高斯滤波的过程,其实和2D卷积是一样的;很显然,双边滤波的计算过程和3D卷积的计算过程也是一样的, 是不是可以借鉴一下呢?
先计算出p(x,y)和q的值,offset作为第三位,像素差作为对应的值,应该也是可以的。但是仔细想想,感觉哪里不太对, 相当于卷积核在发生变化?
A Fast Approximation of the Bilateral Filter using a Signal Processing Approach
虽然上述原始想法有些问题,但仔细分析后可以发现,不合理的主要原因是|I(p) - I(q)|在发生变化。 然而,再仔细思索一下,虽然值在发生变化,但是取值范围是有限的,如果第三个维度是插值的值域,就可以进行3维卷积操作了。
从想法到落地,还是需要很多工作的,Durand 在 2006 年提出了近似加速算法 使用接近40页的篇幅描述了加速的过程:(还没完全理解,理解后补充一下)
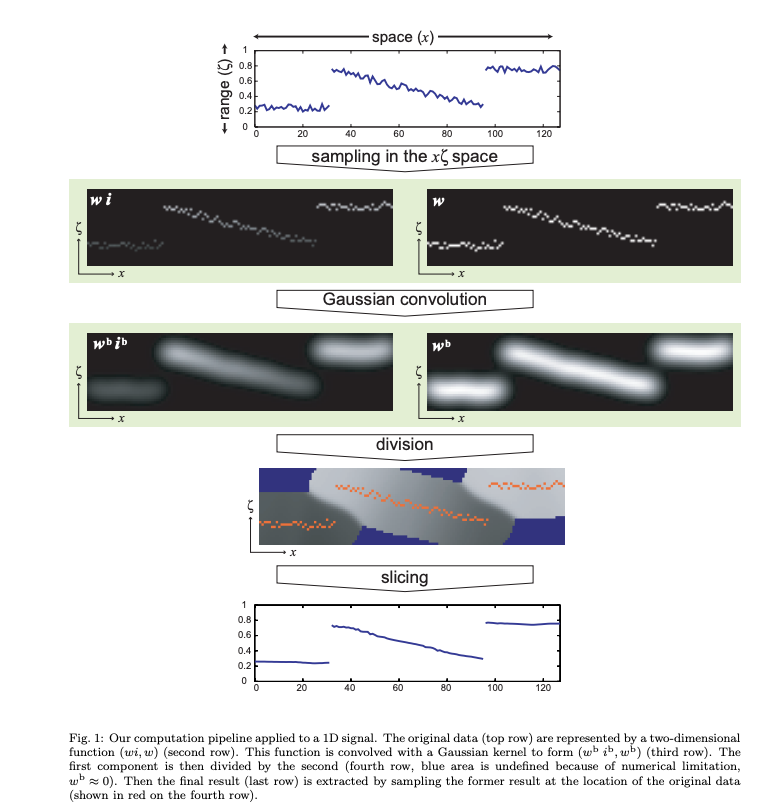
如上图所示,核心思想如下:
- 像素值作为一个额外维度,使得weight的计算转变成第三维度上的卷积,提高了data locality利用率
- 离散化,并使用一个额外的channel记录分母,称之为 homogeneous coordinate(下图右侧一列)
- 使用slicing操作重新得到原数据空间的值
承上启下的过渡: Bilateral Grid
Durand 进一步发展了这个思路,和 Jiawen Chen 一起做了优秀的工作, 将空间域和像素值域都离散化、网格化,提出了 bilateral grid 数据结构, 进一步加速了计算过程。 把之前引入额外维度这个动作背后的思想进一步挖掘深化,为后来的工作铺平了道路。
在这个工作中,将之前提出的 fast approximate 算法中的核心思想提炼出来, 总结成一个新的数据结构 bilateral grid,并且发现很多操作都可以归纳到这个框架内。
使用bilateral grid通常分为三步: 首先,从图像或者其他输入构建网格;在网格内进行变换;对网格进行切片,重构输出。 构建网格和切分网格是图像和网格空间的等价变换。
-
Grid Creation
给出图片I(已经归一化到$[0, 1]$之间),$s_s$表示空间采样率, $s_r$表示取值的采样率,按照如下方法构建网格$\tau$:
- 初始化:对所有的网格 $(i,j,k), \tau(i,j,k)=(0,0)
- 填充:对于(x,y)位置的每个像素,有:
$[.]$表示取整(四舍五入)操作。使用$\tau = c(I)$表示构建过程。
-
Processing
任何接受三维输入的函数都可以用于对应的网格 ,得到新的网格$\hat{\tau} = f(\tau)$
-
Extracting a 2D Map by Slicing
切片是产生分段平滑输出的关键双边网格操作。给定双边网格$\tau$和参考图片E,我们通过对 $(x/s_s, y/s_s, E(x,y)/s_r$这个位置的网格进行三线性差值来得到对应的值。 使用$M=s_E(\tau)$表示该过程。
上文提到的双边滤波,可以用如下公式表示:
\[bf(I) = s_I(G_{\delta_s, \delta_r} \bigotimes c(I))\]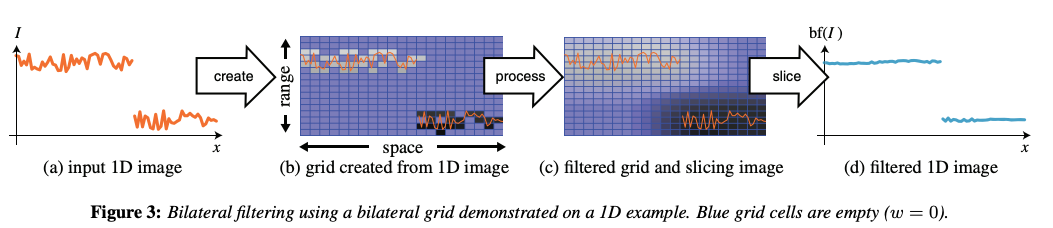
加速多种滤镜的速度:BGU
Chen 和 Durand 在此基础上继续发展,利用 bilateral grid 的思想,加速其他滤镜, 做出了 Bilateral Guided Upsample (BGU) 这样优秀的工作。
由于很多复杂的滤镜处理速度比较慢, 一个很常用的解决思路是对原图 downsample 之后做处理, 然后用 upsample 得到处理结果。 这里 Kaiming He 的 guide filter 就是一个这种思路的很好的应用。 而在 BGU 这个例子里,利用 bilateral grid 来做 downsample - upsample 的工作,使得效果更为出色。
其核心思想是:
- 任何滤镜效果,在局部小区域内都可以看做是一个线性变换
- 利用 bilateral grid 可以从一个低分辨率的图上 slice 得到高分辨率的结果
- upsample 针对的是变换系数,而不是直接针对像素。这样对细节方面损失降低到最小
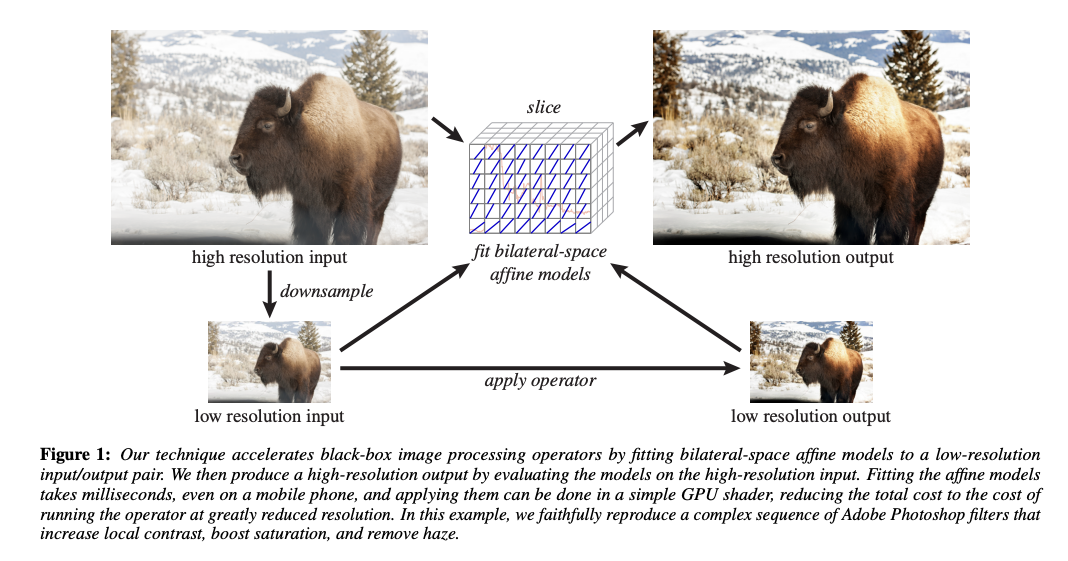
具体实现的步骤如下:
- 对原图 downsample 得到一个小图
- 在小图上应用滤镜
- 在小图上划分网格(bilateral graid),拟合每一个网格中的线性变换
- 线性变换的系数在网格间做平滑
- 利用这个网格,根据原始大图在这个网格上做 slicing,得到高分辨率的线性变换系数,进一步得到高分辨率的结果
这里有两点比较重要, 一是利用 bilaeral grid 做 slicing 来 upsample, 二是用线性变换的系数做中间媒介,而不是直接 upsample 小图。 这样得到的结果更为自然,大图的细节损失很小。
集大成者:HDRnet
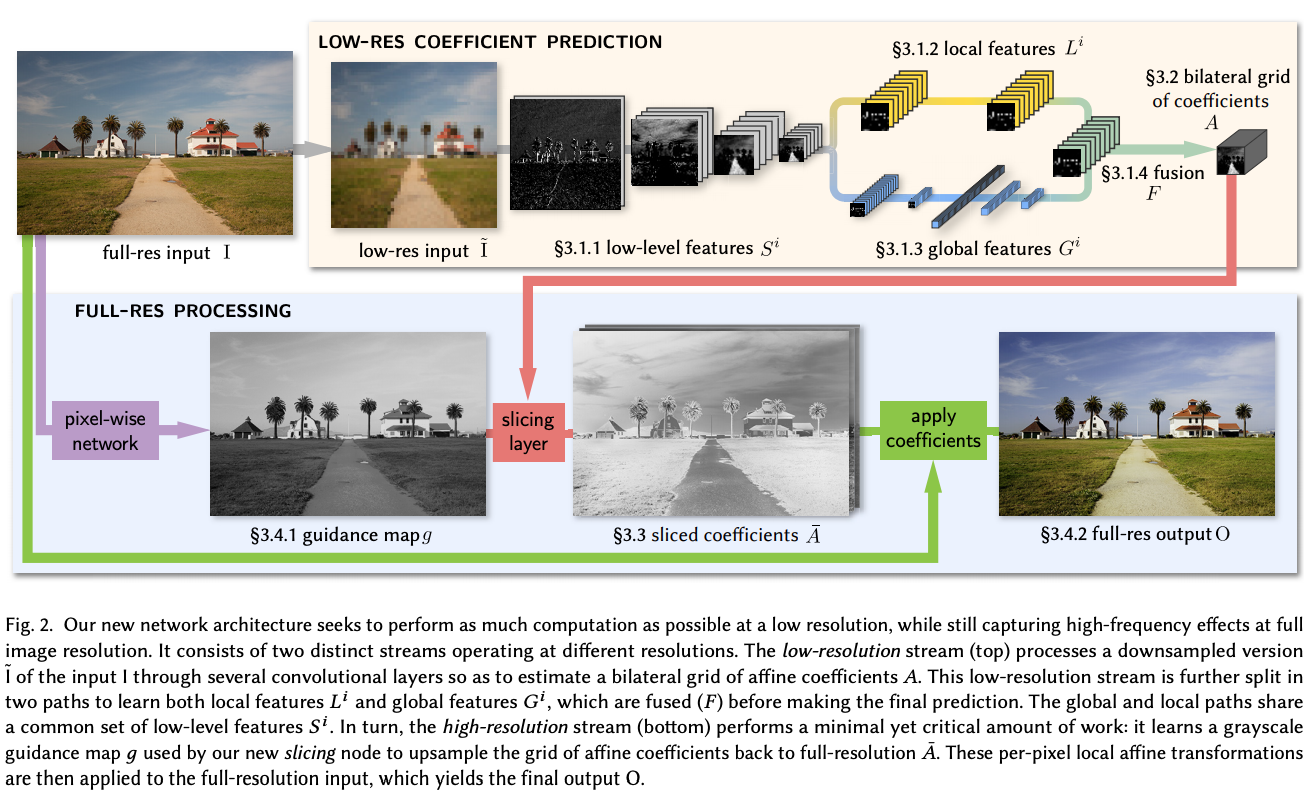
这里重点在右上角黄色背景的这个模块,利用神经网络提取出一系列特征, 包括「低级特征」、「局部特征」和「全局特征」。 所有特征综合起来,得到一系列特征图。 从这些特征图,进一步得到每一张特征图对应的局部线性变换(参见上一小节), 并利用 bilateral grid 存下这些线性变换的系数; 注意,这里的系数对应的是 downsample 后的小图。
在下面蓝色的模块中,首先得到一张「引导图」,参照这个引导图, 在 bilateral grid 中做 sliceing 操作,得到大图的 per pixel 的变换系数 (参见上一小节,对系数 upsample)。最后 apply 这些系数,就得到变换后的输出图像。
这个工作有以下优点:
- 神经网络提取出一系列特征,包含低级特征、局部特征、全局特征。 对于图像处理来说,非常完整。 考虑到人类摄影师修图的过程,也无非考虑这几方面的特征,因此这个方法适用范围非常广。
- 神经网络强大的学习能力,可以学习非常复杂的变换; 局部线性变换的假设,一定程度上防止了过拟合。这个方法鲁棒性很好。
- 相比 BGU 在像素上做线性变换,这里是在神经网络提取的特征上做变换,结果更稳定, 并且能 handle 极为复杂、非线性极强的变换形式 (我猜测,比如可以学习某一个特定摄影师的修图风格 ← 这种非常抽象很难定义的问题)
- 利用 bilateral grid 做 upsample,可以得到较高的质量, 从而在前期可以放心做 downsample, 一方面减少计算量加快计算速度,一方面也防止过拟合到一些局部细节上。